Reshaping and reorganizing data#
Reshaping and reorganizing data refers to the process of changing the structure or organization of data by modifying dimensions, array shapes, order of values, or indexes. Xarray provides several methods to accomplish these tasks.
These methods are particularly useful for reshaping xarray objects for use in machine learning packages, such as scikit-learn, that usually require two-dimensional numpy arrays as inputs. Reshaping can also be required before passing data to external visualization tools, for example geospatial data might expect input organized into a particular format corresponding to stacks of satellite images.
Importing the library#
Reordering dimensions#
To reorder dimensions on a DataArray or across all variables
on a Dataset, use transpose(). An
ellipsis (…) can be used to represent all other dimensions:
In [1]: ds = xr.Dataset({"foo": (("x", "y", "z"), [[[42]]]), "bar": (("y", "z"), [[24]])})
In [2]: ds.transpose("y", "z", "x")
Out[2]:
<xarray.Dataset> Size: 16B
Dimensions: (x: 1, y: 1, z: 1)
Dimensions without coordinates: x, y, z
Data variables:
foo (y, z, x) int64 8B 42
bar (y, z) int64 8B 24
In [3]: ds.transpose(..., "x") # equivalent
Out[3]:
<xarray.Dataset> Size: 16B
Dimensions: (x: 1, y: 1, z: 1)
Dimensions without coordinates: x, y, z
Data variables:
foo (y, z, x) int64 8B 42
bar (y, z) int64 8B 24
In [4]: ds.transpose() # reverses all dimensions
Out[4]:
<xarray.Dataset> Size: 16B
Dimensions: (x: 1, y: 1, z: 1)
Dimensions without coordinates: x, y, z
Data variables:
foo (z, y, x) int64 8B 42
bar (z, y) int64 8B 24
Expand and squeeze dimensions#
To expand a DataArray or all
variables on a Dataset along a new dimension,
use expand_dims()
In [5]: expanded = ds.expand_dims("w")
In [6]: expanded
Out[6]:
<xarray.Dataset> Size: 16B
Dimensions: (w: 1, x: 1, y: 1, z: 1)
Dimensions without coordinates: w, x, y, z
Data variables:
foo (w, x, y, z) int64 8B 42
bar (w, y, z) int64 8B 24
This method attaches a new dimension with size 1 to all data variables.
To remove such a size-1 dimension from the DataArray
or Dataset,
use squeeze()
In [7]: expanded.squeeze("w")
Out[7]:
<xarray.Dataset> Size: 16B
Dimensions: (x: 1, y: 1, z: 1)
Dimensions without coordinates: x, y, z
Data variables:
foo (x, y, z) int64 8B 42
bar (y, z) int64 8B 24
Converting between datasets and arrays#
To convert from a Dataset to a DataArray, use to_dataarray():
In [8]: arr = ds.to_dataarray()
In [9]: arr
Out[9]:
<xarray.DataArray (variable: 2, x: 1, y: 1, z: 1)> Size: 16B
array([[[[42]]],
[[[24]]]])
Coordinates:
* variable (variable) object 16B 'foo' 'bar'
Dimensions without coordinates: x, y, z
This method broadcasts all data variables in the dataset against each other, then concatenates them along a new dimension into a new array while preserving coordinates.
To convert back from a DataArray to a Dataset, use
to_dataset():
In [10]: arr.to_dataset(dim="variable")
Out[10]:
<xarray.Dataset> Size: 16B
Dimensions: (x: 1, y: 1, z: 1)
Dimensions without coordinates: x, y, z
Data variables:
foo (x, y, z) int64 8B 42
bar (x, y, z) int64 8B 24
The broadcasting behavior of to_dataarray means that the resulting array
includes the union of data variable dimensions:
In [11]: ds2 = xr.Dataset({"a": 0, "b": ("x", [3, 4, 5])})
# the input dataset has 4 elements
In [12]: ds2
Out[12]:
<xarray.Dataset> Size: 32B
Dimensions: (x: 3)
Dimensions without coordinates: x
Data variables:
a int64 8B 0
b (x) int64 24B 3 4 5
# the resulting array has 6 elements
In [13]: ds2.to_dataarray()
Out[13]:
<xarray.DataArray (variable: 2, x: 3)> Size: 48B
array([[0, 0, 0],
[3, 4, 5]])
Coordinates:
* variable (variable) object 16B 'a' 'b'
Dimensions without coordinates: x
Otherwise, the result could not be represented as an orthogonal array.
If you use to_dataset without supplying the dim argument, the DataArray will be converted into a Dataset of one variable:
In [14]: arr.to_dataset(name="combined")
Out[14]:
<xarray.Dataset> Size: 32B
Dimensions: (variable: 2, x: 1, y: 1, z: 1)
Coordinates:
* variable (variable) object 16B 'foo' 'bar'
Dimensions without coordinates: x, y, z
Data variables:
combined (variable, x, y, z) int64 16B 42 24
Stack and unstack#
As part of xarray’s nascent support for pandas.MultiIndex, we have
implemented stack() and
unstack() method, for combining or splitting dimensions:
In [15]: array = xr.DataArray(
....: np.random.randn(2, 3), coords=[("x", ["a", "b"]), ("y", [0, 1, 2])]
....: )
....:
In [16]: stacked = array.stack(z=("x", "y"))
In [17]: stacked
Out[17]:
<xarray.DataArray (z: 6)> Size: 48B
array([ 0.469, -0.283, -1.509, -1.136, 1.212, -0.173])
Coordinates:
* z (z) object 48B MultiIndex
* x (z) <U1 24B 'a' 'a' 'a' 'b' 'b' 'b'
* y (z) int64 48B 0 1 2 0 1 2
In [18]: stacked.unstack("z")
Out[18]:
<xarray.DataArray (x: 2, y: 3)> Size: 48B
array([[ 0.469, -0.283, -1.509],
[-1.136, 1.212, -0.173]])
Coordinates:
* x (x) <U1 8B 'a' 'b'
* y (y) int64 24B 0 1 2
As elsewhere in xarray, an ellipsis (…) can be used to represent all unlisted dimensions:
In [19]: stacked = array.stack(z=[..., "x"])
In [20]: stacked
Out[20]:
<xarray.DataArray (z: 6)> Size: 48B
array([ 0.469, -1.136, -0.283, 1.212, -1.509, -0.173])
Coordinates:
* z (z) object 48B MultiIndex
* y (z) int64 48B 0 0 1 1 2 2
* x (z) <U1 24B 'a' 'b' 'a' 'b' 'a' 'b'
These methods are modeled on the pandas.DataFrame methods of the
same name, although in xarray they always create new dimensions rather than
adding to the existing index or columns.
Like DataFrame.unstack, xarray’s unstack
always succeeds, even if the multi-index being unstacked does not contain all
possible levels. Missing levels are filled in with NaN in the resulting object:
In [21]: stacked2 = stacked[::2]
In [22]: stacked2
Out[22]:
<xarray.DataArray (z: 3)> Size: 24B
array([ 0.469, -0.283, -1.509])
Coordinates:
* z (z) object 24B MultiIndex
* y (z) int64 24B 0 1 2
* x (z) <U1 12B 'a' 'a' 'a'
In [23]: stacked2.unstack("z")
Out[23]:
<xarray.DataArray (y: 3, x: 1)> Size: 24B
array([[ 0.469],
[-0.283],
[-1.509]])
Coordinates:
* y (y) int64 24B 0 1 2
* x (x) <U1 4B 'a'
However, xarray’s stack has an important difference from pandas: unlike
pandas, it does not automatically drop missing values. Compare:
In [24]: array = xr.DataArray([[np.nan, 1], [2, 3]], dims=["x", "y"])
In [25]: array.stack(z=("x", "y"))
Out[25]:
<xarray.DataArray (z: 4)> Size: 32B
array([nan, 1., 2., 3.])
Coordinates:
* z (z) object 32B MultiIndex
* x (z) int64 32B 0 0 1 1
* y (z) int64 32B 0 1 0 1
In [26]: array.to_pandas().stack()
Out[26]:
x y
0 1 1.0
1 0 2.0
1 3.0
dtype: float64
We departed from pandas’s behavior here because predictable shapes for new array dimensions is necessary for Parallel computing with Dask.
Stacking different variables together#
These stacking and unstacking operations are particularly useful for reshaping
xarray objects for use in machine learning packages, such as scikit-learn, that usually require two-dimensional numpy
arrays as inputs. For datasets with only one variable, we only need stack
and unstack, but combining multiple variables in a
xarray.Dataset is more complicated. If the variables in the dataset
have matching numbers of dimensions, we can call
to_dataarray() and then stack along the the new coordinate.
But to_dataarray() will broadcast the dataarrays together,
which will effectively tile the lower dimensional variable along the missing
dimensions. The method xarray.Dataset.to_stacked_array() allows
combining variables of differing dimensions without this wasteful copying while
xarray.DataArray.to_unstacked_dataset() reverses this operation.
Just as with xarray.Dataset.stack() the stacked coordinate is
represented by a pandas.MultiIndex object. These methods are used
like this:
In [27]: data = xr.Dataset(
....: data_vars={"a": (("x", "y"), [[0, 1, 2], [3, 4, 5]]), "b": ("x", [6, 7])},
....: coords={"y": ["u", "v", "w"]},
....: )
....:
In [28]: data
Out[28]:
<xarray.Dataset> Size: 76B
Dimensions: (x: 2, y: 3)
Coordinates:
* y (y) <U1 12B 'u' 'v' 'w'
Dimensions without coordinates: x
Data variables:
a (x, y) int64 48B 0 1 2 3 4 5
b (x) int64 16B 6 7
In [29]: stacked = data.to_stacked_array("z", sample_dims=["x"])
In [30]: stacked
Out[30]:
<xarray.DataArray 'a' (x: 2, z: 4)> Size: 64B
array([[0, 1, 2, 6],
[3, 4, 5, 7]])
Coordinates:
* z (z) object 32B MultiIndex
* variable (z) object 32B 'a' 'a' 'a' 'b'
* y (z) object 32B 'u' 'v' 'w' nan
Dimensions without coordinates: x
In [31]: unstacked = stacked.to_unstacked_dataset("z")
In [32]: unstacked
Out[32]:
<xarray.Dataset> Size: 88B
Dimensions: (y: 3, x: 2)
Coordinates:
* y (y) object 24B 'u' 'v' 'w'
Dimensions without coordinates: x
Data variables:
a (x, y) int64 48B 0 1 2 3 4 5
b (x) int64 16B 6 7
In this example, stacked is a two dimensional array that we can easily pass to a scikit-learn or another generic
numerical method.
Note
Unlike with stack, in to_stacked_array, the user specifies the dimensions they do not want stacked.
For a machine learning task, these unstacked dimensions can be interpreted as the dimensions over which samples are
drawn, whereas the stacked coordinates are the features. Naturally, all variables should possess these sampling
dimensions.
Set and reset index#
Complementary to stack / unstack, xarray’s .set_index, .reset_index and
.reorder_levels allow easy manipulation of DataArray or Dataset
multi-indexes without modifying the data and its dimensions.
You can create a multi-index from several 1-dimensional variables and/or
coordinates using set_index():
In [33]: da = xr.DataArray(
....: np.random.rand(4),
....: coords={
....: "band": ("x", ["a", "a", "b", "b"]),
....: "wavenumber": ("x", np.linspace(200, 400, 4)),
....: },
....: dims="x",
....: )
....:
In [34]: da
Out[34]:
<xarray.DataArray (x: 4)> Size: 32B
array([0.123, 0.543, 0.373, 0.448])
Coordinates:
band (x) <U1 16B 'a' 'a' 'b' 'b'
wavenumber (x) float64 32B 200.0 266.7 333.3 400.0
Dimensions without coordinates: x
In [35]: mda = da.set_index(x=["band", "wavenumber"])
In [36]: mda
Out[36]:
<xarray.DataArray (x: 4)> Size: 32B
array([0.123, 0.543, 0.373, 0.448])
Coordinates:
* x (x) object 32B MultiIndex
* band (x) <U1 16B 'a' 'a' 'b' 'b'
* wavenumber (x) float64 32B 200.0 266.7 333.3 400.0
These coordinates can now be used for indexing, e.g.,
In [37]: mda.sel(band="a")
Out[37]:
<xarray.DataArray (wavenumber: 2)> Size: 16B
array([0.123, 0.543])
Coordinates:
* wavenumber (wavenumber) float64 16B 200.0 266.7
band <U1 4B 'a'
Conversely, you can use reset_index()
to extract multi-index levels as coordinates (this is mainly useful
for serialization):
In [38]: mda.reset_index("x")
Out[38]:
<xarray.DataArray (x: 4)> Size: 32B
array([0.123, 0.543, 0.373, 0.448])
Coordinates:
band (x) <U1 16B 'a' 'a' 'b' 'b'
wavenumber (x) float64 32B 200.0 266.7 333.3 400.0
Dimensions without coordinates: x
reorder_levels() allows changing the order
of multi-index levels:
In [39]: mda.reorder_levels(x=["wavenumber", "band"])
Out[39]:
<xarray.DataArray (x: 4)> Size: 32B
array([0.123, 0.543, 0.373, 0.448])
Coordinates:
* x (x) object 32B MultiIndex
* wavenumber (x) float64 32B 200.0 266.7 333.3 400.0
* band (x) <U1 16B 'a' 'a' 'b' 'b'
As of xarray v0.9 coordinate labels for each dimension are optional.
You can also use .set_index / .reset_index to add / remove
labels for one or several dimensions:
In [40]: array = xr.DataArray([1, 2, 3], dims="x")
In [41]: array
Out[41]:
<xarray.DataArray (x: 3)> Size: 24B
array([1, 2, 3])
Dimensions without coordinates: x
In [42]: array["c"] = ("x", ["a", "b", "c"])
In [43]: array.set_index(x="c")
Out[43]:
<xarray.DataArray (x: 3)> Size: 24B
array([1, 2, 3])
Coordinates:
* x (x) <U1 12B 'a' 'b' 'c'
In [44]: array = array.set_index(x="c")
In [45]: array = array.reset_index("x", drop=True)
Shift and roll#
To adjust coordinate labels, you can use the shift() and
roll() methods:
In [46]: array = xr.DataArray([1, 2, 3, 4], dims="x")
In [47]: array.shift(x=2)
Out[47]:
<xarray.DataArray (x: 4)> Size: 32B
array([nan, nan, 1., 2.])
Dimensions without coordinates: x
In [48]: array.roll(x=2, roll_coords=True)
Out[48]:
<xarray.DataArray (x: 4)> Size: 32B
array([3, 4, 1, 2])
Dimensions without coordinates: x
Sort#
One may sort a DataArray/Dataset via sortby() and
sortby(). The input can be an individual or list of
1D DataArray objects:
In [49]: ds = xr.Dataset(
....: {
....: "A": (("x", "y"), [[1, 2], [3, 4]]),
....: "B": (("x", "y"), [[5, 6], [7, 8]]),
....: },
....: coords={"x": ["b", "a"], "y": [1, 0]},
....: )
....:
In [50]: dax = xr.DataArray([100, 99], [("x", [0, 1])])
In [51]: day = xr.DataArray([90, 80], [("y", [0, 1])])
In [52]: ds.sortby([day, dax])
Out[52]:
<xarray.Dataset> Size: 88B
Dimensions: (x: 2, y: 2)
Coordinates:
* x (x) <U1 8B 'b' 'a'
* y (y) int64 16B 1 0
Data variables:
A (x, y) int64 32B 1 2 3 4
B (x, y) int64 32B 5 6 7 8
As a shortcut, you can refer to existing coordinates by name:
In [53]: ds.sortby("x")
Out[53]:
<xarray.Dataset> Size: 88B
Dimensions: (x: 2, y: 2)
Coordinates:
* x (x) <U1 8B 'a' 'b'
* y (y) int64 16B 1 0
Data variables:
A (x, y) int64 32B 3 4 1 2
B (x, y) int64 32B 7 8 5 6
In [54]: ds.sortby(["y", "x"])
Out[54]:
<xarray.Dataset> Size: 88B
Dimensions: (x: 2, y: 2)
Coordinates:
* x (x) <U1 8B 'a' 'b'
* y (y) int64 16B 0 1
Data variables:
A (x, y) int64 32B 4 3 2 1
B (x, y) int64 32B 8 7 6 5
In [55]: ds.sortby(["y", "x"], ascending=False)
Out[55]:
<xarray.Dataset> Size: 88B
Dimensions: (x: 2, y: 2)
Coordinates:
* x (x) <U1 8B 'b' 'a'
* y (y) int64 16B 1 0
Data variables:
A (x, y) int64 32B 1 2 3 4
B (x, y) int64 32B 5 6 7 8
Reshaping via coarsen#
Whilst coarsen is normally used for reducing your data’s resolution by applying a reduction function
(see the page on computation),
it can also be used to reorganise your data without applying a computation via construct().
Taking our example tutorial air temperature dataset over the Northern US
In [56]: air = xr.tutorial.open_dataset("air_temperature")["air"]
In [57]: air.isel(time=0).plot(x="lon", y="lat")
Out[57]: <matplotlib.collections.QuadMesh at 0x7f9250d96950>
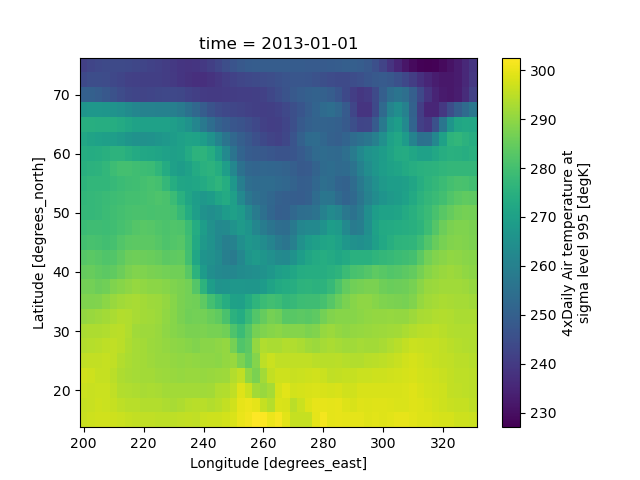
we can split this up into sub-regions of size (9, 18) points using construct():
In [58]: regions = air.coarsen(lat=9, lon=18, boundary="pad").construct(
....: lon=("x_coarse", "x_fine"), lat=("y_coarse", "y_fine")
....: )
....:
In [59]: regions
Out[59]:
<xarray.DataArray 'air' (time: 2920, y_coarse: 3, y_fine: 9, x_coarse: 3,
x_fine: 18)> Size: 34MB
array([[[[[241.2 , 242.5 , 243.5 , ..., 238.7 , 239.6 , 241. ],
[242.89, 244.8 , 246.5 , ..., 248.6 , 249. , 249.5 ],
[249.6 , 249.1 , 247.8 , ..., 235.5 , 238.6 , nan]],
[[243.8 , 244.5 , 244.7 , ..., 237.1 , 237.2 , 238. ],
[239.3 , 240.7 , 242. , ..., 244.3 , 243.89, 244. ],
[244.6 , 245.6 , 246.8 , ..., 235.3 , 239.3 , nan]],
[[250. , 249.8 , 248.89, ..., 241. , 240.1 , 239.7 ],
[239.8 , 240.1 , 240.39, ..., 249.1 , 246.8 , 243.7 ],
[240.6 , 239.1 , 240.2 , ..., 236.39, 241.7 , nan]],
...,
[[273.7 , 273.6 , 273.79, ..., 275.5 , 276. , 273.7 ],
[269. , 262.7 , 256.2 , ..., 252.89, 252.5 , 254.3 ],
[258.1 , 262.29, 265.1 , ..., 274.2 , 275.1 , nan]],
[[274.79, 275.2 , 275.6 , ..., 272.79, 274.9 , 275.5 ],
[273.79, 269. , 261.9 , ..., 253.6 , 252.7 , 253. ],
...
[289.89, 290.59, 291.19, ..., 295.69, 295.69, 295.49],
[296.19, 297.19, 297.09, ..., 292.49, 292.09, nan]],
[[291.49, 291.39, 292.39, ..., 291.19, 290.99, 291.39],
[291.89, 292.99, 294.59, ..., 297.29, 297.69, 298.19],
[298.59, 298.29, 297.89, ..., 293.09, 293.19, nan]],
...,
[[297.69, 298.09, 298.09, ..., 297.79, 298.39, 298.89],
[298.99, 298.89, 299.19, ..., 299.89, 300.19, 300.29],
[300.09, 300.39, 300.69, ..., 296.19, 295.69, nan]],
[[ nan, nan, nan, ..., nan, nan, nan],
[ nan, nan, nan, ..., nan, nan, nan],
[ nan, nan, nan, ..., nan, nan, nan]],
[[ nan, nan, nan, ..., nan, nan, nan],
[ nan, nan, nan, ..., nan, nan, nan],
[ nan, nan, nan, ..., nan, nan, nan]]]]])
Coordinates:
lat (y_coarse, y_fine) float32 108B 75.0 72.5 70.0 ... 15.0 nan nan
lon (x_coarse, x_fine) float32 216B 200.0 202.5 205.0 ... 330.0 nan
* time (time) datetime64[ns] 23kB 2013-01-01 ... 2014-12-31T18:00:00
Dimensions without coordinates: y_coarse, y_fine, x_coarse, x_fine
Attributes:
long_name: 4xDaily Air temperature at sigma level 995
units: degK
precision: 2
GRIB_id: 11
GRIB_name: TMP
var_desc: Air temperature
dataset: NMC Reanalysis
level_desc: Surface
statistic: Individual Obs
parent_stat: Other
actual_range: [185.16 322.1 ]
9 new regions have been created, each of size 9 by 18 points.
The boundary="pad" kwarg ensured that all regions are the same size even though the data does not evenly divide into these sizes.
By plotting these 9 regions together via faceting we can see how they relate to the original data.
In [60]: regions.isel(time=0).plot(
....: x="x_fine", y="y_fine", col="x_coarse", row="y_coarse", yincrease=False
....: )
....:
Out[60]: <xarray.plot.facetgrid.FacetGrid at 0x7f9250b91060>
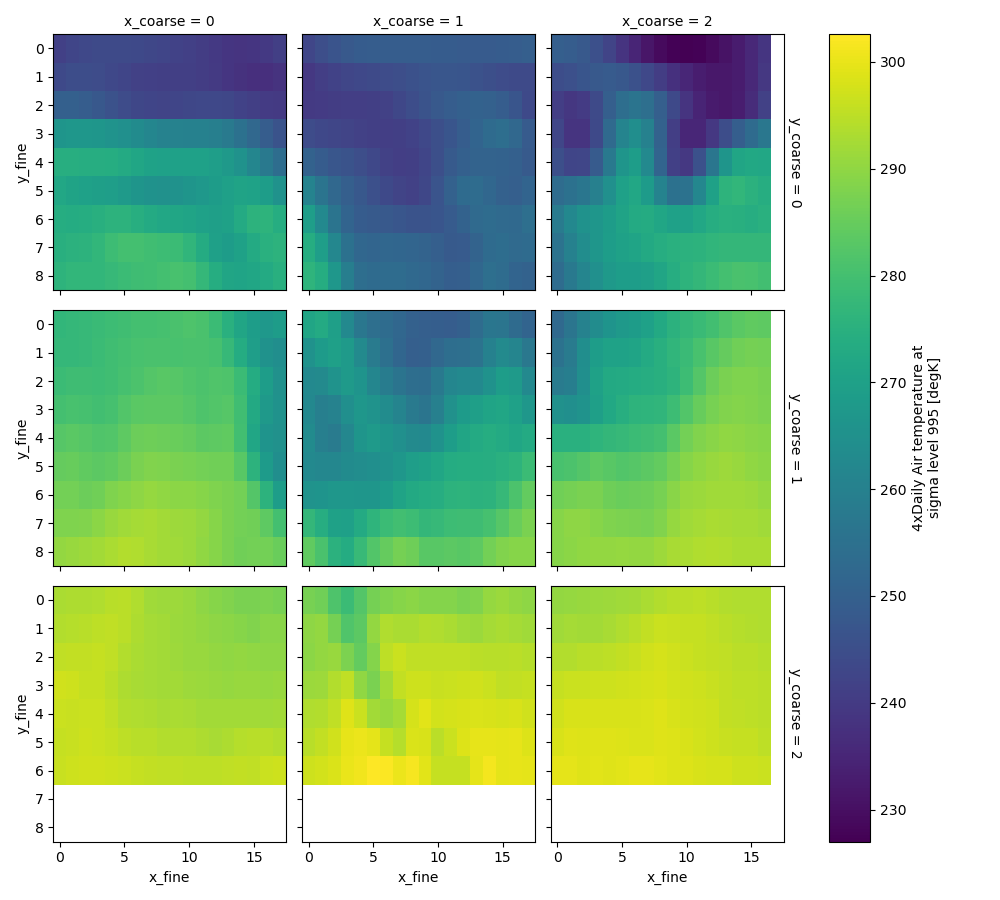
We are now free to easily apply any custom computation to each coarsened region of our new dataarray.
This would involve specifying that applied functions should act over the "x_fine" and "y_fine" dimensions,
but broadcast over the "x_coarse" and "y_coarse" dimensions.